Cross-domain Few-shot Learning with Task-specific Adapters

CVPR 2022

Wei-Hong Li, Xialei Liu and Hakan Bilen

        

Abstract

In this paper, we look at the problem of cross-domain few-shot classification that aims to learn a classifier from previously unseen classes and domains with few labeled samples. Recent approaches broadly solve this problem by parameterizing their few-shot classifiers with task-agnostic and task-specific weights where the former is typically learned on a large training set and the latter is dynamically predicted through an auxiliary network conditioned on a small support set. In this work, we focus on the estimation of the latter, and propose to learn task-specific weights from scratch directly on a small support set, in contrast to dynamically estimating them. In particular, through systematic analysis, we show that task-specific weights through parametric adapters in matrix form with residual connections to multiple intermediate layers of a backbone network significantly improves the performance of the state-of-the-art models in the Meta-Dataset benchmark with minor additional cost.

Few-shot Learning

Few-shot classification aims at learning a model that can be efficiently adapted to recognize unseen classes from few samples. Broadly, recent approaches address this challenge by parameterizing deep networks with a large set of task-agnostic and a small set of task-specific weights that encode generic representations valid for multiple tasks and private representations are specific to the target task respectively. While the task-agnostic weights are learned over multiple tasks, typically, from a large dataset in meta-training, the task-specific weights are estimated from a given small support set (e.g. 5 images per category).

Figure 1. Cross-domain Few-shot Learning considers to learn a model from one or multiple domains to generalize to unseen domains with few samples.

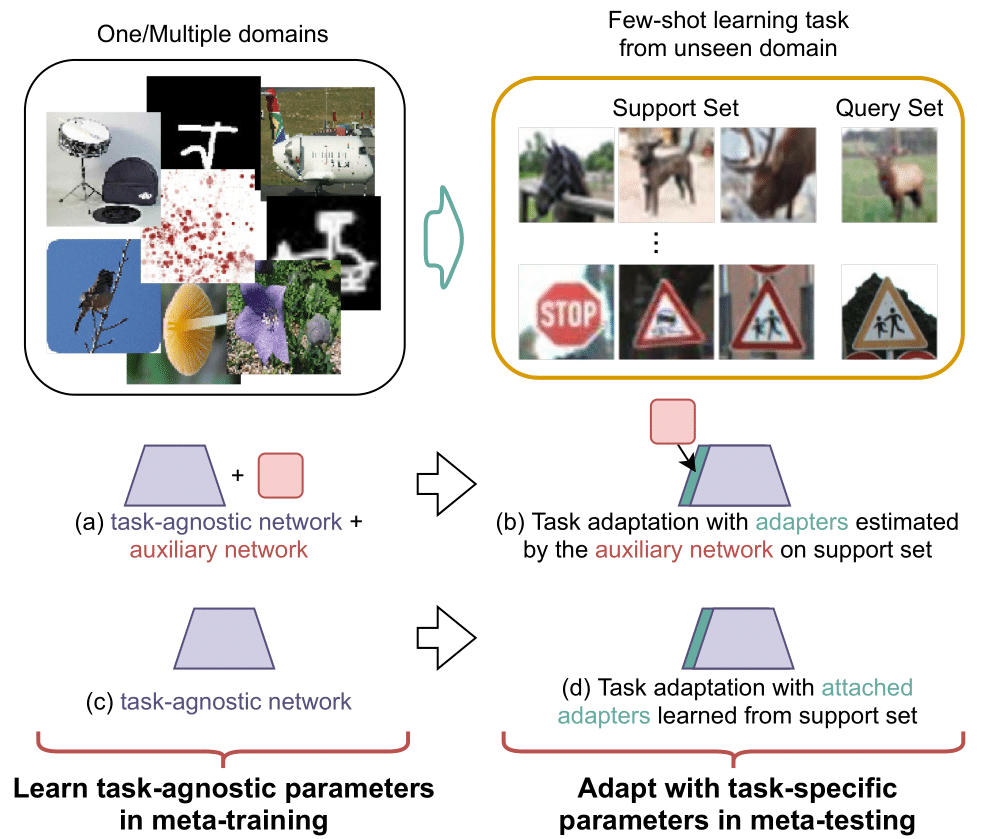
Prior works often learn a task-agnostic model with an auxiliary network during meta-training Figure 1(a) and a set of adapters are generated by the auxiliary network to adapt to the given support set Figure 1(b). While in this work, we propose to attach adapters directly to a pretrained task-agnostic model Figure 1(c), which can be estimated from scratch during meta-testing Figure 1(d). We also propose different architecture topologies of adapters and their efficient approximations.

Task-agnostic Representation Learning

Learning task-agnostic or universal representations has been key to the success of cross-domain generalization. Representations learned from a large diverse dataset such as ImageNet can be considered as universal and successfully transferred to tasks in different domains with minor adaptations. We denote this setting as single domain learning (SDL).

More powerful and diverse representations can be obtained by training a single network over multiple domains. Let \(\mathcal{D}_{b}=\{\mathcal{D}_{k}\}_{k=1}^{K}\) consists of \(K\) subdatasets, each sampled from a different domain. The vanilla multi-domain learning (MDL) strategy jointly optimizes network parameters over the images from all \(K\) subdatasets:

\(\min_{\phi, \psi_{k}} \sum_{k=1}^{K} \frac{1}{|\mathcal{D}_{k}|} \sum_{\mathbf{x}, y \in \mathcal{D}_{k}} \ell(g_{\psi_{k}} \circ f_{\phi}(\mathbf{x}), y),\)

where \(\ell\) is cross-entropy loss, \(f\) is feature extractor that takes an image as input and outputs a \(d\) dimensional feature. \(f\) is parameterized by \(\phi\) which is shared across \(K\) domains. \(g_{\psi_{k}}\) is the classifier for domain \(k\) and parameterized by \(\psi_k\) which is discarded in meta-test. We denote this setting as MDL.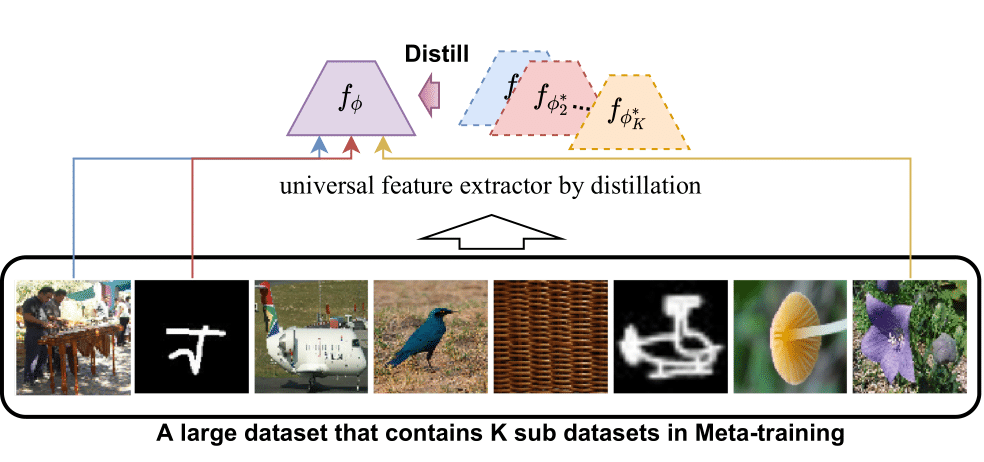

Figure 2. URL - Universal Representation Learning. Learning a single universal feature extractor \(f_{\phi}\) that is distilled from multiple feature extractors \(\{f_{\phi^{\ast}_\tau}\}_{\tau}^{K}\) during meta-training.

The challenge in MDL is to allow efficiently sharing the knowledge across the domains while preventing negative transfer between them and also carefully balancing the individual loss functions. URL [7] (our prior work as illustrated in Figure 2), a variant of MDL, mitigates these challenges by first training individual domain-specific networks offline and then distilling their knowledge into a single multi-domain network. See this post for more details.

Task-specific Adapter Parameterization

To this end, one can learn a single task-agnostic network \(f_{\phi}\) during the meta-training over one or multiple domains and in this work, we investigate different task adaptation strategies for cross-domain few-shot learning. We show that directly attach adapters in matrix form with residual connection and learn them from scratch on the support set obtains the best performance.

To obtain the task-specific weights, we freeze the task-agnostic weights \(\phi\) and minimize the cross-entropy loss \(\ell\) over the support samples in meta-test w.r.t. the task-specific weights \(\vartheta\):

\(\min_{\vartheta}\frac{1}{|\mathcal{S}|}\sum_{(\mathbf{x}, y) \in \mathcal{S}} \ell(p_{(\phi,\vartheta)}(\mathbf{x}),y),\)

where \(\mathcal{S}\) is sampled from the test set \(\mathcal{D}_t\). A simple method to adapt \(f_{\phi}\) is finetuning its parameters on the support set. However, this strategy tends to suffer from the unproportionate optimization, i.e. updating very high-dimensional weights from a small number of support samples.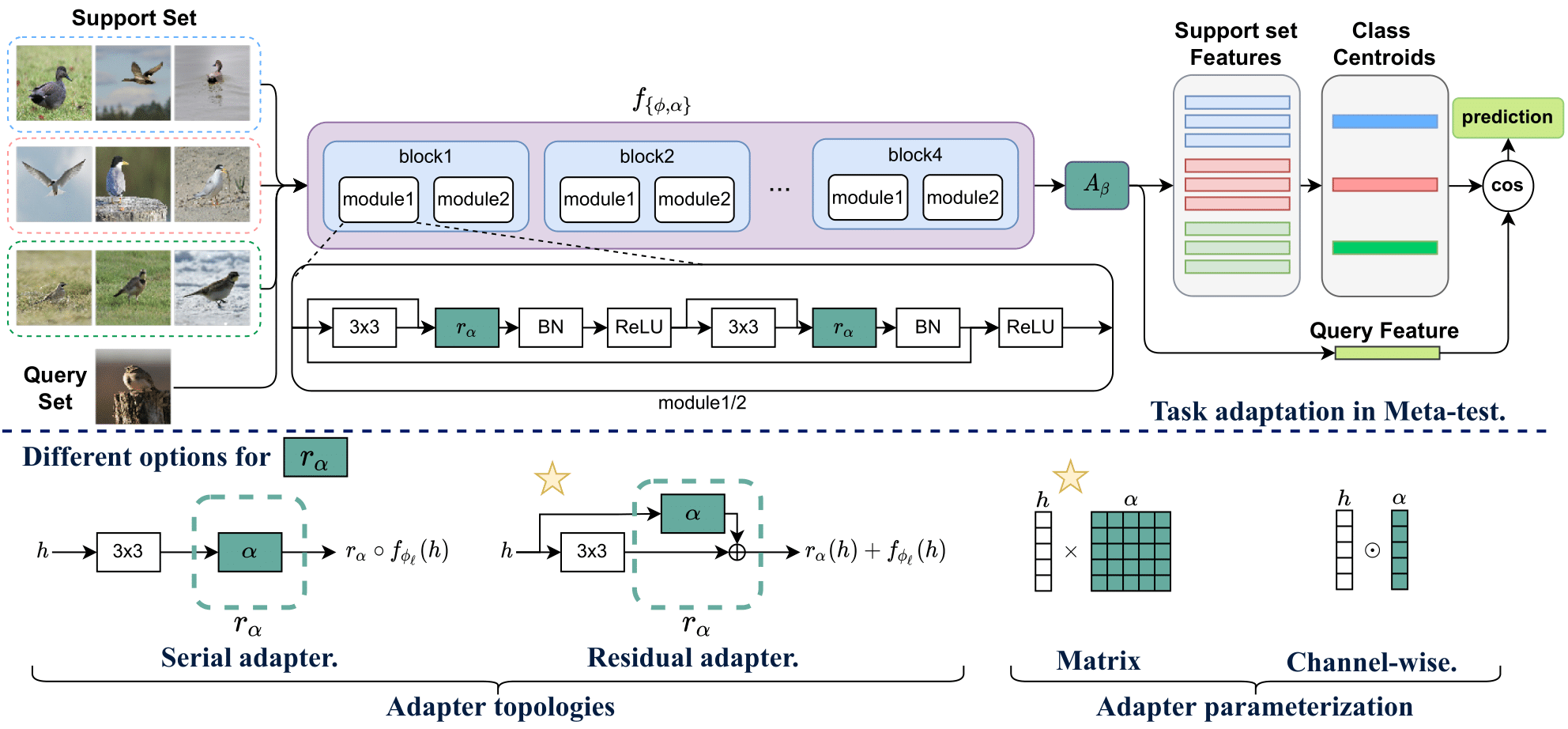

Figure 3. Illustration of our task adaptation for cross-domain few-shot learning. In meta-test stage (a), our method first attaches a parametric transformation \(r_{\alpha}\) to each layer, where \(\alpha\) can be constructed by (b) a serial or (c) a residual topology. They can be parameterized with matrix multiplication (d) or channel-wise scaling (e). We found that (c) is the best configuration with matrix parameterization which is further improved by attaching a linear transformation \(A_{\beta}\) to the end of the network. We adapt the network for a given task by optimizing \(\alpha\) and \(A_{\beta}\) on a few labeled images from the support set, then map query images to the task-specific space and assign them to the nearest class center.

To this end, we propose to attach task-specific adapters directly to the existing task-agnostic model, e.g. we attach the adapters to each module of a ResNet backbone in Figure 3 (a), and the adapters can be efficiently learned/estimated from few samples.

Concretely, let \(f_{\phi_l}\) denote the \(l\)-th layer of the task-agnostic feature extractor \(f_{\phi}\), (i.e. a convolutional layer) with the weights \(\phi_l\). Given a support set \(\mathcal{S}\), the task-specific adapters \(r_{\alpha}\) parameterized by \(\alpha\), can be incorporated to the output of the layer \(f_{\phi_l}\) as:

\(f_{\{\phi_l,\alpha\}}(\mathbf{h}) = r_{\alpha}(f_{\phi_l}(\mathbf{h}),\mathbf{h})\)

where \(\mathbf{h}\in\mathrm{R}^{W\times H \times C}\) is the input tensor, \(f_{\phi_l}\) is a convolutional layer in \(f_{\phi}\). Importantly, the number of the task-specific adaptation parameters \(\alpha\) are significantly smaller than the task-agnostic ones.

The adapters can be designed in different ways. We propose two connection types for incorporating \(r_\alpha\) to \(f_{\phi_l}\): i) serial connection by subsequently applying it to the output of layer \(f_{\phi_l}(\mathbf{h})\) as: \[ f_{\{\phi_l,\alpha\}}(\mathbf{h}) = r_{\alpha} \circ f_{\phi_l}(\mathbf{h}) \] which is illustrated in Figure 3(b), and ii) parallel connection by a residual addition as in [8]: \[ f_{\{\phi_l,\alpha\}}(\mathbf{h}) = r_{\alpha}(\mathbf{h}) + f_{\phi_l}(\mathbf{h}) \] which is illustrated in Figure 3(c). In our experiments, we found the parallel setting performing the best when \(\alpha\) is learned on a support set during meta-test (illustrated in Figure 3(c)).

For the parameterization of \(r_{\alpha}\), we consider two options. Matrix multiplication (illustrated in Figure 3(d)) with \(\alpha\in\mathrm{R}^{C\times C}\): \(r_{\alpha}(\mathbf{h}) = \mathbf{h} \ast \alpha\), where \(\ast\) denotes a convolution, \(\alpha\in \mathbb{R}^{C\times C}\) and the transformation is implemented as a convolutional operation with \(1\times 1\) kernels. And channelwise scaling (illustrated in Figure 3(e)): \( r_{\alpha}(\mathbf{h}) = \mathbf{h} \odot \alpha, \) where \(\odot\) is a Hadamard product and \(\alpha\in \mathbb{R}^C\). Please refer to our paper for more details.

Results

We evaluate our method on Meta-dataset [1]. Please refer to our paper and the leaderboard of Meta-dataset for more results.

Comparison with SOTA

We first compare our method with existing state-of-the-art methods in Meta-dataset [1]. In Figure 4, we can see that, in multi-domain learning setting (i.e. learning the task-agnostic model from multiple domains and evaluate on all domains), our method (i.e. attach residual adapters in matrix form to URL [7]) performs much better than the state-of-the-art methods, especially obtaining significant improvement in unseen domains. Also, in Figure 5, we evaluate our method in single-domain learning setting where we use a standard single-domain learning model learned from ImageNet as task-agnostic model and adapt the features with residual adapters in matrix form. Here we follow the settings in FLUTE [5] and CTX [9], use ResNet-18 as backbone when comparing our method with FLUTE and use ResNet-34 for the comparison with CTX. We can see that adapting the features with residual adapters in matrix form also obtains the best performance in single-domain learning setting with different backbones.

Figure 4. Comparisons with FLUTE [5], tri-M [6], URL [7] in multi-domain learning setting in Meta-dataset.

Figure 5. Comparisons with FLUTE [5] and CTX [9] in single-domain learning setting in Meta-dataset.

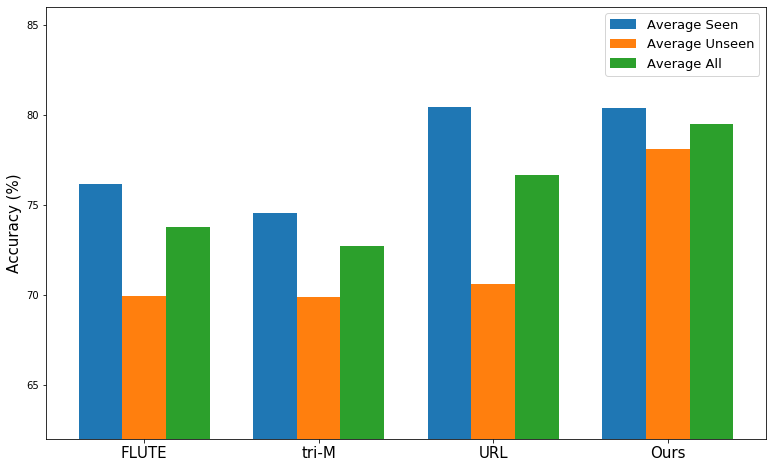
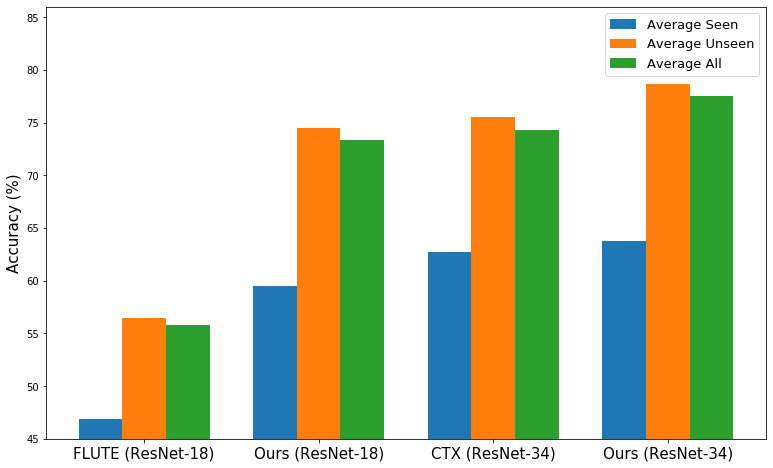
Analysis

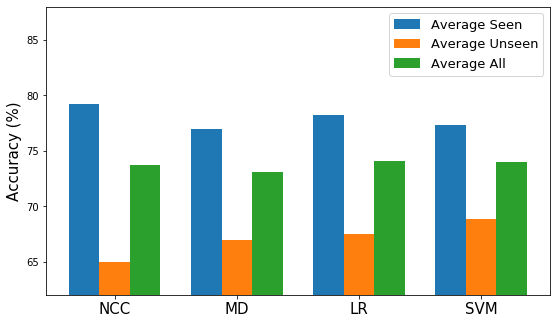
Here we evaluate different task adaptation strategies in Meta-dataset. We use the URL as task-agnostic model and freeze the weight of URL and only optimize the task-specific parameters (if any). We first compare learning different type of classifiers on top of the features, including NCC (nearest centroid classifier), MD (Mahalanobis distance), LR (logistic regression) and SVM (support vector machines). We can see that in overall, NCC performs the best and it requires no additional parameters. To this end, we then evaluate other adaptation techniques with NCC.

Figure 6. Comparisons of different classifiers. NCC, MD, LR, SVM denote nearest centroid classifier, Mahalanobis distance, logistic regression, support vector machines respectively.

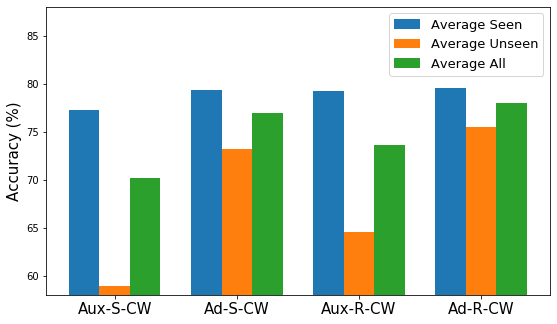
We then compare different ways of estimating task-specific adapters, including using Auxiliary (Aux) network or directly attaching adapters (Ad) in serial (S) or residual (R) connection in Figure 7. From the results, we can see that directly attaching and learning adapters from scratch on the support set performs better than using an auxiliary network to estimate dadapters as it is difficult to learn a very accurate auxiliary network for previously unseen tasks. We also observe that the adaptation strategies using residual connections performs better than the serial one in almost all cases, and the gains are more substantial when generalizing to unseen domains.

Figure 7. Comparisons of ways to estimate task-specific adapters. 'Aux' and 'Ad' indicate using an auxiliary network to estimate adapters or directly attaching adapters to the network and learning them from scratch on the support set, respecitvely. 'S' and 'R' means serial and residual connection, respectively. 'CW' means channel-wise scaling adapters parameterization.

We then investigate different topologies and parameterizations of task-specific adapters when adapting the features by directly attaching task-specific adapters to the network and learning them on the support set. We summarize the results in Figure 8. Here, we can see that residual connections are more effective than the serial ones and the performance can be further improved by using the adapters in matrix form. Also, the pre-classifier alignment can further boost the performance. Please refer to our paper for more detailed analysis and discussions.

Figure 8. Comparisons of task-specific adapters' topologies and parameterizations. 'Ad' indicates directly attaching adapters to the network and learning them from scratch on the support set, respecitvely. 'S' and 'R' means serial and residual connection, respectively. 'M' and 'CW' mean matrix or channel-wise scaling adapters parameterization, respectively. 'PA' indicates pre-classifier alignment mapping.

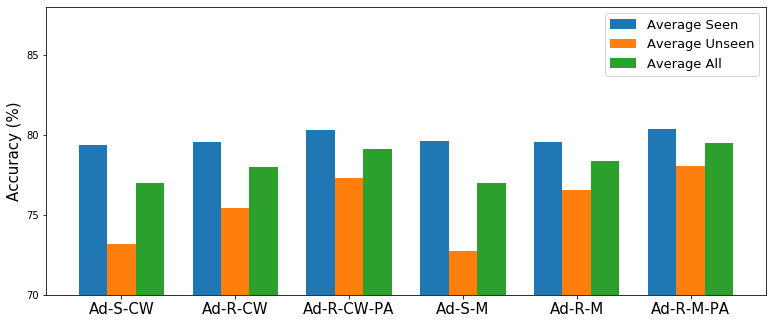
Qualitative Results

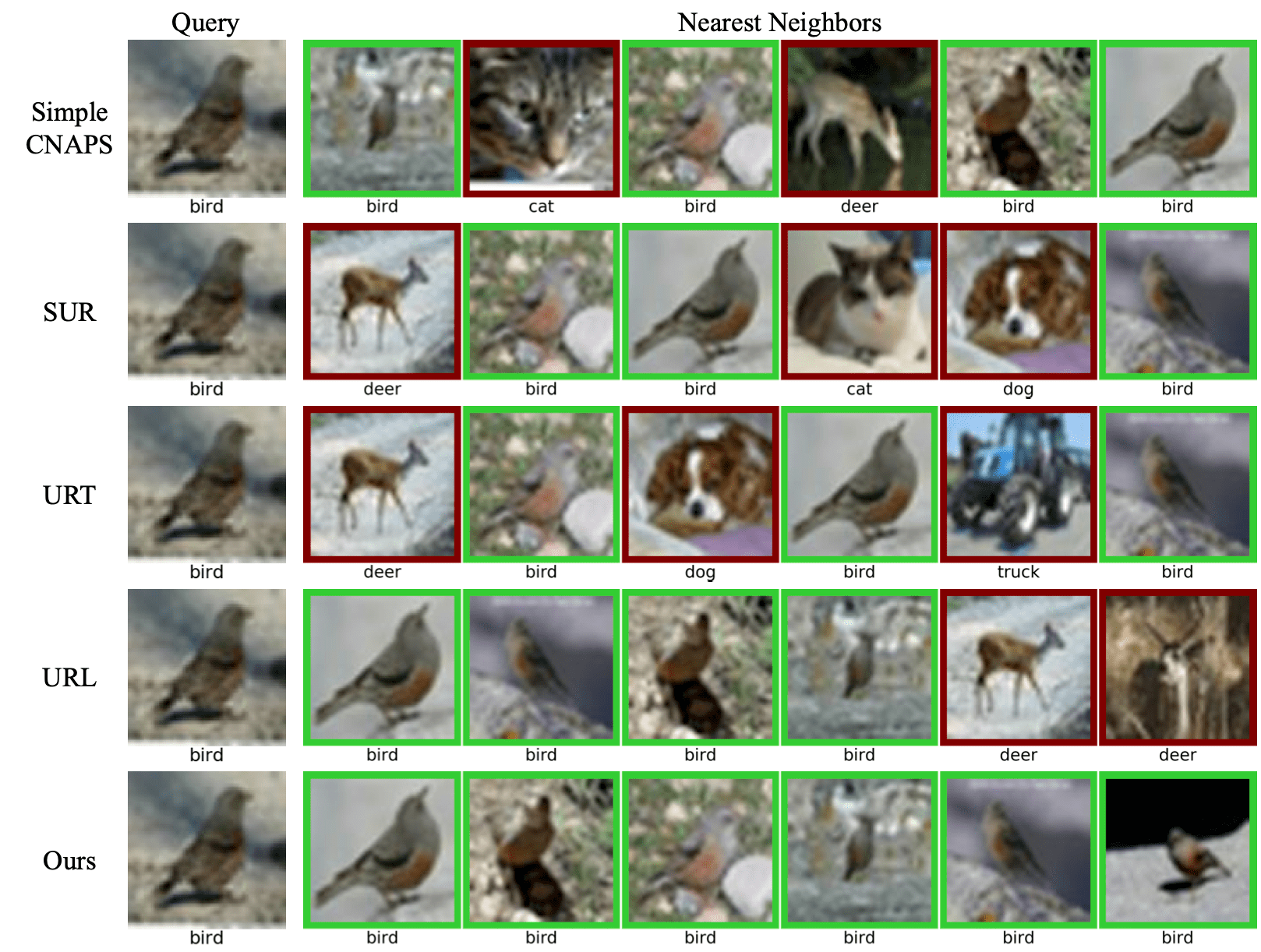
We also qualitatively analyze our method and compare it to Simple CNAPS, SUR, URT, and URL in Figure 9 by illustrating the nearest neighbors in CIFAR-10 (unseen domain) given a query image (see supplementary for more examples). Though URL learns more generalized features from multiple domains, it still suffer from the distration of colors, shapes and backgrounds. Our method learns the light weight task-specific adapters to adapt the features such that our method is able to retrieve semantically similar images and finds more correct neighbors than URL. It again suggests that our method is able to efficiently adapt the features to be more semantically meaningful and general.

Figure 9. Qualitative comparisons of our method and state-of-the-art approaches (Simple CNAPS [2], SUR [3], URT [4], URL [7]) in CIFAR-10 (unseen dataset).

Reference

[1] Eleni Triantafillou, Tyler Zhu, Vincent Dumoulin, Pascal Lamblin, Utku Evci, Kelvin Xu, Ross Goroshin, Carles Gelada, Kevin Swersky, Pierre-Antoine Manzagol, Hugo Larochelle; Meta-Dataset: A Dataset of Datasets for Learning to Learn from Few Examples; ICLR 2020.

[2] Peyman Bateni, Raghav Goyal, Vaden Masrani, Frank Wood, Leonid Sigal; Improved Few-Shot Visual Classification; CVPR 2020.

[3] Nikita Dvornik, Cordelia Schmid, Julien Mairal; Selecting Relevant Features from a Multi-domain Representation for Few-shot Classification; ECCV 2020.

[4] Lu Liu, William Hamilton, Guodong Long, Jing Jiang, Hugo Larochelle; Universal Representation Transformer Layer for Few-Shot Image Classification; ICLR 2021.

[5] Eleni Triantafillou, Hugo Larochelle, Richard Zemel, Vincent Dumoulin; Learning a Universal Template for Few-shot Dataset Generalization; ICML 2021.

[6] Yanbin Liu, Juho Lee, Linchao Zhu, Ling Chen, Humphrey Shi, Yi Yang; A Multi-Mode Modulator for Multi-Domain Few-Shot Classification; ICCV 2021.

[7] Wei-Hong Li, Xialei Liu, Hakan Bilen; Universal Representation Learning from Multiple Domains for Few-shot Classification; ICCV 2021.

[8] Sylvestre-Alvise Rebuffi, Hakan Bilen, Andrea Vedaldi; Efficient parametrization of multi-domain deep neural networks; CVPR 2018.

[9] Carl Doersch, Ankush Gupta, Andrew Zisserman; CrossTransformers: spatially-aware few-shot transfer; NeurIPS 2020.