Introduction

In recent years, a considerable amount of research has been carried out into the prediction and certification of resource usage of computer programs. The term resource refers to some quantity which can be regarded as a cost of the program. Typical resources include quantities such as time and heap space usage, but other quantities such as the number of SMS messages sent by a Java application installed on a mobile phone have also been considered.

In RESA, we are concentrating on static analysis techniques because these enable reliable guarantees to be produced without requiring a program to be executed; thus the resource usage of a program can be evaluated before it is even installed on its target platform.

Techniques

We are using two main high-level analysis techniques: amortised analysis and lattice-point enumeration in polytopes. These are supported by lower-level abstract interpretation methods.

Amortised analysis

Amortised resource analysis is based on Tarjan’s observation [1] that the statement and proof of complexity bounds for operations on some data structures can be simplified if we think of the elements of the data structure as being able to store “credits” which are used up by later operations. We have shown how amortisation techniques can be combined with Separation Logic to reason about resource usage associated with complex data structures: see [2] for details.

An analysis technique which predicts resource usage using linear programming in conjunction with the techniques described above has also been developed and implemented.

Lattice points

Amortisation techniques are useful for dealing with resources associated with data structures, but are less useful for nested loop structures controlled by numerical program variables. We have been exploring the use of geometric techniques to predict the resource usage of such structures.

Consider the following fragment of a Java program:

       for (i=1; i<=9; i++)
         for (j=1; j<=i && j<=7; j++)
           System.out.println ("Hello");

How many times is the println statement executed? (More generally, we might be allocating memory or sending an SMS message.) Note that every time println is encountered we have the inequalities 1 ≤ i ≤ 9, 1 ≤ j ≤ 7, and j ≤ i, which delineate a trapezoidal region in the (i,j)-plane:

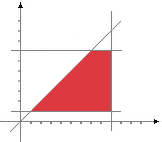
It is easily seen that the number of times that the println statement is executed is equal to the number of lattice points (points with integer coordinates: move your mouse over the image) within the region. There is a rich mathematical theory dealing with the problem of counting lattice points within regions described by linear constraints [3,4] and we are implementing a resource analysis using these techniques.

Ultimately we hope to combine amortised analysis with lattice-point enumeration in order to obtain a method which will enable automatic resource analysis of a wide range of Java bytecode programs.

Tools

We intend to develop a static analysis tool for Java bytecode programs. We are implementing a stand-alone command-line based tool in the OCaml functional programming language, and eventually we plan to incorporate this into a plugin for the eclipse Java development environment. Since eclipse is widely used by Java programmers, this will make our tool available to programmers in a straightforward way in a familiar environment. See [5] for more information.

References

1. Robert E. Tarjan. Amortized computational complexity.
SIAM Journal on Algebraic Discrete Methods, Vol. 6, No. 2. (April 1985), pp. 306-318.

2. Robert Atkey. Amortised Resource Analysis with Separation Logic.
To appear in the proceedings of ESOP 2010.
Download PDF.

3. Alexander Barvinok, James E. Pommersheim. An Algorithmic Theory of Lattice Points in Polyhedra.
New Perspectives in Algebraic Combinatorics, MSRI Publications, 38, 1999, 91-147.
Download PS.

4. Matthias Beck, Sinai Robbins. Computing the Continuous Discretely.
Springer-Verlag, 2007.
Link.

5. David Aspinall, Robert Atkey, Kenneth MacKenzie and Don Sannella. Symbolic and Analytic Techniques for Resource Analysis of Java Bytecode.
To appear in the Proceedings of TGC 2010.
Download PDF.